Differentiate (x2 – 5x + 8) (x3 + 7x + 9) in three ways mentioned below:
(i) by using product rule
(ii) by expanding the product to obtain a single polynomial.
(iii) by logarithmic differentiation.
Do they all give the same answer?
Given: (x2 – 5x + 8) (x3 + 7x + 9)
Let y=(x2 – 5x + 8) (x3 + 7x + 9)
(i) By applying product rule differentiate both sides with respect to x
![]()
![]()
![]()
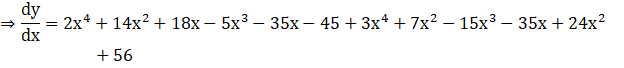
![]()
(ii) by expanding the product to obtain a single polynomial
y = (x2 – 5x + 8) (x3 + 7x + 9)
y = x5 + 7x3 + 9x2 - 5x4 – 35x2 - 45x + 8x3 + 56x + 72
y = x5 - 5x4 + 15x3 - 26x2 + 11x + 72
Now, differentiate both sides with respect to x
![]()
![]()
(iii) by logarithmic differentiation
y = (x2 – 5x + 8) (x3 + 7x + 9)
Taking log on both sides, we get
log y = log ((x2 – 5x + 8) (x3 + 7x + 9))
log y = log (x2 – 5x + 8) + log (x3 + 7x + 9)
Now, differentiate both sides with respect to x
![]()
![]()
![]()
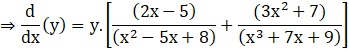
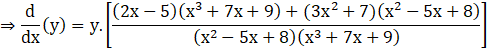
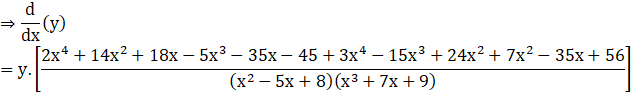
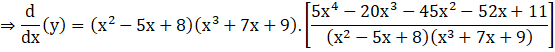
![]()
From equation (i),(ii)and(iii), we can say that value of given function after differentiating by all the three methods is same.