If 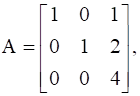 then show that |3A| = 27|A|
then show that |3A| = 27|A|
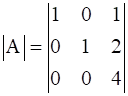
We know that a determinant of a 3 x 3 matrix is calculated as
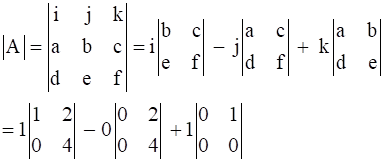
= 1[1(4) - 2(0)] – 0 + 1[0-0]
= 1[4 - 0] – 0 + 0
= 4
|A|= 4
LHS: |3A|
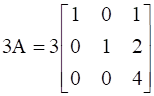
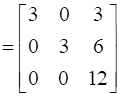
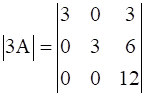
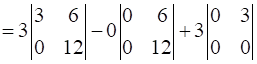
= 3[3(12) - 0(6)] – 0 + 3[0 – 0]
= 3(36) – 0 + 0
= 108
|3A| = 108 ----LHS
RHS: 27|A|
27|A| = 27(4)
= 108
27|A| = 108 ----RHS
LHS=RHS
Hence proved.
15