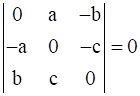
R1→ cR1 (i.e. replace 1st row by multiplying it with c)
As we are multiplying we should also divide c so that the original given determinant is not changed
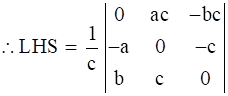
R1→ R1 - bR2 (i.e. replace 1st row by subtraction of 1st row and b times 2nd row)
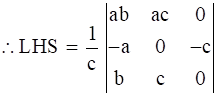
Taking a outside the determinant from 1st row
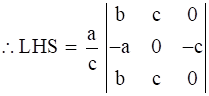
If any two rows or columns of a determinant are identical then the value of that determinant is 0 because we get a row or column with all elements 0 when we when we subtract those particular rows/columns here the transformation is R1 → R1 - R3
∴LHS = 0 = RHS
∴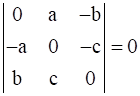
8