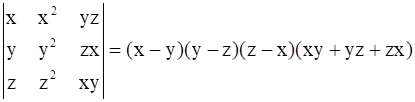
R1 → R1 - R2 (i.e. Replacing 1st row by subtraction of 1st and 2nd row)
R2 → R2 - R3 (i.e. Replacing 2nd row by subtraction of 2nd and 3rd row)
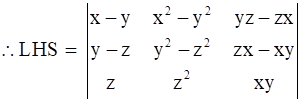
We know x2 - y2 = (x + y)(x - y) and y2 - z2 = (y + z)(y - z)
Therefore taking (x - y) and (y - z) outside the determinant from 1st and 2nd row respectively
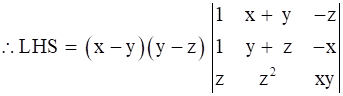
R1 → R1 - R2 (i.e. Replacing 1st row by subtraction of 1st and 2nd row)
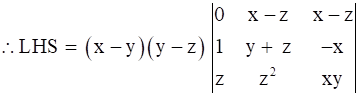
Taking (x - z) outside determinant from 1st row
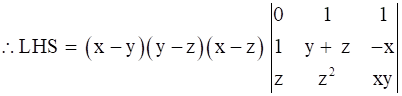
C2 → C2 - C3 (i.e. Replacing 2nd column by subtraction of 2nd and 3rd column)
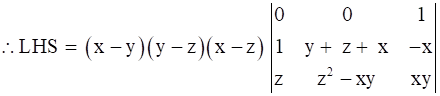
Expanding the determinant along 1st row
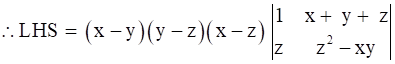
∴ LHS = (x - y)(y - z)(x - z)(z2 - xy - xz - yz - z2)
Cancelling z2 and adjusting the negative sign with (x - z)
∴LHS = (x - y)(y - z)(z - x)(xy + yz + zx) = RHS
∴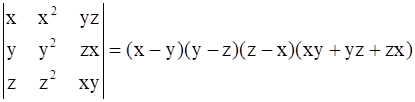
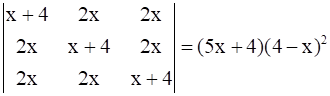
12