Find area of the triangle with vertices at the point given in each of the following:

Question

Find area of the triangle with vertices at the point given in each of the following: (1, 0), (6, 0), (4, 3)

Philoid · Accepted Answer

Given vertices of the triangle are (1, 0), (6, 0), (4, 3)

Let the vertices of the triangle be given by (x₁, y₁), (x₂, y₂), (x₃, y₃)

Area of triangle is given by Δ =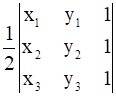

Area of triangle = Δ =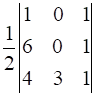

Expanding the determinant along Row 1

Δ = 1/2 × [1 × (0 × 1 – 3 × 1) – 0 × (6 × 1 – 4 × 1) + 1 × (6 × 3 – 4 × 0)]

Δ = 1/2 × [1 × (0 – 3) – 0 + 1 × (18 – 0)]

Δ = 1/2 × (-3 + 18) = 15/2 sq. units

∴ Δ = 15/2 sq. units = 7.5 sq. units