Given vertices of the triangle are A (a, b + c), B (b, c + a), C (c, a + b)

Let the vertices of the triangle be given by (x₁, y₁), (x₂, y₂), (x₃, y₃)

Area of triangle is given by Δ =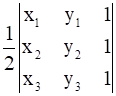

For points to be collinear area of triangle = Δ = 0

So, we have to show that area of triangle formed by ABC is 0

Area of triangle = Δ =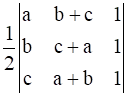

Expanding the determinant along Row 1

Δ = 1/2 × [a × {(c + a) × 1 – (a + b) × 1) – (b + c) × {b × 1 – c × 1} + 1 × {b × (a + b) – c × (c +a)}]

Δ = 1/2 × [a × (c + a – a – b) – (b + c) × (b – c) + 1 × (ab + b² – c² - ca)]

Δ = 1/2 × [a × (c – b) – (b² – c²) + 1 × (ab + b² – c² – ca)]

Δ = 1/2 × (ac – ab – b² + c² + ab + b² – c² – ca) sq units

Δ = 1/2 × 0 sq units

∴ Δ = 0

∴ Given vertices of the triangle are A (a, b + c), B (b, c + a), C (c, a + b) are collinear