Given vertices of the triangle are (k, 0), (4, 0), (0, 2)

Let the vertices of the triangle be given by (x₁, y₁), (x₂, y₂), (x₃, y₃)

Area of triangle is given by Δ =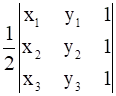

Given, Area of triangle = Δ = 4 sq. units

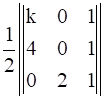= 4

⇒ 4 = 1/2 |[k × (0 × 1 – 2 × 1) – 0 × (4 × 1 – 0 × 1) + 1 × (4 × 2 – 0 × 0)]|

⇒ 4 = 1/2 × |[k × (0 – 2) – 0 + 1 × (8 – 0)]|

⇒ � 4 × 2 = -2k + 8

⇒ 8 = -2k + 8 and -8 = -2k + 8

⇒ 8 – 8 = -2k and 8 + 8 = 2k

⇒ 2k = 0 and 16 = 2k

⇒ k = 0 and k = 8