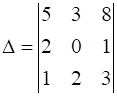
To evaluate a determinant using cofactors, Let

B =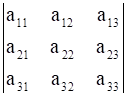

Expanding along Row 1

B =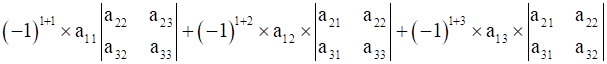

B = a₁₁ A₁₁ + a₁₂ A₁₂ + a₁₃ A₁₃

[Where A_ij represents cofactors of a_ij of determinant B.]

B = Sum of product of elements of R₁ with their corresponding cofactors

Similarly, the determinant can be solved by expanding along column

So, B = sum of product of elements of any row or column with their corresponding cofactors

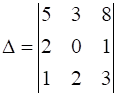
Cofactors of second row

A₂₁ = (-1)²⁺¹ × M₂₁ = (-1) × 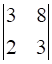= (-1) × (3 × 3 – 8 × 2) = (-1) × (-7) = 7

A₂₂ = (-1)²⁺² × M₂₂ = 1 × 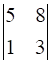= (5 × 3 – 8 × 1) = 7

A₂₃ = (-1)²⁺³ × M₂₃ = (-1) × 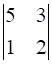= (-1) × (5 × 2 – 3 × 1) = (-1) × 7 = -7

[Where A_ij = (-1)^i+j × M_ij, M_ij = Minor of i^th row & j^th column]

Therefore,

Δ = a₂₁A₂₁ + a₂₂A₂₂ + a₂₃A₂₃

Δ = 2 × 7 + 1 × (-7) = 14 - 7 = 7

Ans: Δ = 7