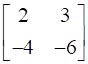
Adjoint of the matrix A = [a_ij]_n×n is defined as the transpose of the matrix [A_ij]_n×n where A_ij is the co-factor of the element a_ij.

Let’s find the cofactors for all the positions first-

Here, A₁₁ = -6, A₁₂ = 4, A₂₁ = -3, A₂₂ = 2.

∴ Adj A =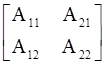

=

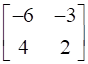
So LHS = A(AdjA) =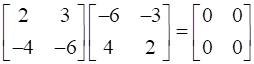

Also AdjA(A) =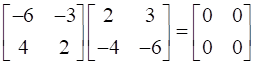

Determinant of A = |A| = 2(-6)-(3)(-4) = 0

So RHS = |A|I = 0

Hence A(AdjA) = AdjA(A) = |A|I = 0 {hence proved}