If ![]() for , – 1 < x < 1, prove that
for , – 1 < x < 1, prove that 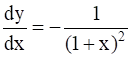
Given, ![]()
![]()
Now, squaring both sides, we get
⇒ ![]()
⇒ ![]()
⇒ x2 + x2y = y2 + y2x
⇒ x2 – y2 = xy2 – x2y
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = –xy
⇒ y + xy = –x
⇒ y (1 + x) = –x
⇒ ![]()
Differentiating both sides with respect to x, we get
![]()
Using Quotient Rule
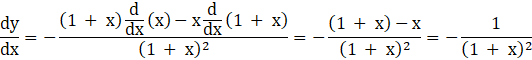
∴ ![]()
Hence, Proved
17