If (x – a) 2 + (y – b) 2 = c 2 , for some c 0, prove that 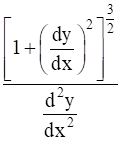is a constant independent of a and b.

Question

If (x – a) 2 + (y – b) 2 = c 2 , for some c > 0, prove that is a constant independent of a and b.

Philoid · Accepted Answer

Given, (x – a)² + (y – b)² = c²

Differentiating with respect to x, we get

⇒

∴

Differentiating again with respect to x

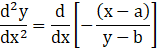
Using Quotient Rule

⇒

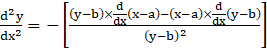
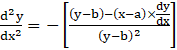
Substituting the value of dy/dx in the above equation

⇒

∴

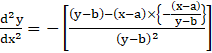
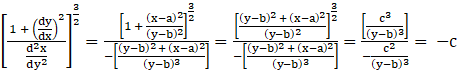
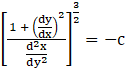∴ , which is independent of a and b

Hence, Proved