Using mathematical induction prove that 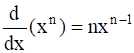 for all positive integers n.
for all positive integers n.
To prove : P(n) : ![]() = nxn – 1 for all positive integers n
= nxn – 1 for all positive integers n
For n = 1,
LHS = ![]() = 1
= 1
RHS = 1 × x1 – 1 = 1
So, LHS = RHS
∴ P(1) is true.
∴ P(n) is true for n = 1
Let P(k) be true for some positive integer k.
i.e. P(k) = ![]()
Now, to prove that P(k + 1) is also true
RHS = (k + 1)x(k + 1) – 1
LHS = ![]()
![]()
![]()
![]()
![]()
![]()
∴ LHS = RHS
Thus, P(k + 1) is true whenever P(k) is true.
Therefore, by the principle of mathematical induction, the statement P(n) is true for every positive integer n.
Hence, proved.
19