Considering the function

f(x) = |x| + |x + 1|

The above function f is continuous everywhere, but is not differentiable at x = 0 and x = – 1

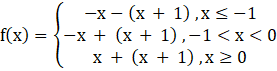
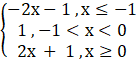
Now, checking continuity

CASE I: At x < – 1

f(x) = – 2x – 1

f(x) is a polynomial

⇒ f(x) is continuous [∵ Every polynomial function is continuous]

CASE II: x > 0

f(x) = 2x + 1

f(x) is a polynomial

⇒ f(x) is continuous [∵ Every polynomial function is continuous]

CASE III: At – 1 < x < 0

f(x) = 1

f(x) is constant

⇒ f(x) is continuous

CASE IV: At x = – 1

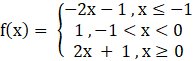
A function will be continuous at x = – 1

If LHL = RHL = f( – 1)

i.e.

LHL =

Putting x = – 1

LHL = – 2 × ( – 1) – 1 = 2 – 1 = 1

RHL =

f(x) = – 2x – 1

f( – 1) = – 2 × ( – 1) – 1 = 2 – 1 = 1

so, LHL = RHL = f( – 1)

⇒ f is continuous.

CASE V: At x = 0

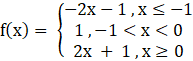
A function will be continuous at x = 0

If LHL = RHL = f(0)

i.e.

LHL = = 1

RHL =

Putting x = 0

RHL = 2 × 0 + 1 = 1

f(x) = 2x + 1

f(0) = 2 × 0 + 1 = 0 + 1 = 1

so, LHL = RHL = f(0)

⇒ f is continuous.

Thus f(x) = |x| + |x + 1| is continuous for all values of x.

Checking differentiability

CASE I: At x < – 1

f(x) = – 2x – 1

f’(x) = – 2

f(x) is polynomial.

⇒ f(x) is differentiable

CASE II: At x > 0

f(x) = 2x + 1

f’(x) = 2

f(x) is polynomial.

⇒ f(x) is differentiable

CASE III: At – 1 < x < 0

f(x) = 1

f(x) is constant.

⇒ f(x) is differentiable

CASE IV: At x = – 1

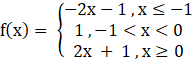
f is differentiable at x = – 1 if

LHD = RHD = f’( – 1)

i.e.

LHD =

LHD =

RHD =

Since, LHD ≠ RHD

∴ f is not differentiable at x = – 1

CASE V: At x = 0

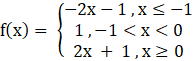
f is differentiable at x = 0 if

LHD = RHD = f’(0)

i.e.

LHD =

RHD =

Since, LHD ≠ RHD

∴ f is not differentiable at x = 0

So, f is not differentiable at exactly two point x = 0 and x = 1, but continuous at all points.