Which of the following functions are strictly decreasing on 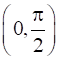 ?
?
A. cos x
B. cos 2x
C. cos 3x
D. tan x
(A) Let f1(x) = cosx
![]()
In interval![]() ,
, ![]()
Therefore, f1(x) = cosx is strictly decreasing in interval![]() .
.
(B) Let f2(x) = cos2x
![]()
Now, 0 < x < ![]()
⇒ 0 < 2x < π
⇒ sin2x > 0
⇒ -2sin2x < 0
![]()
Therefore, f2(x) = cos2x is strictly decreasing in interval![]() .
.
(C) Let f3(x) = cos3x
![]()
Now, ![]()
⇒ sin3x = 0
⇒ 3x = π, as xϵ![]()
⇒ x = ![]()
The point x =![]() divides the interval
divides the interval ![]() into two distinct intervals.
into two distinct intervals.
i.e. ![]() and
and ![]()
Now, in interval, ![]() ,
,
f3'(x) = -3sin3x < 0 as (0 < x < ![]() => 0 < 3x < π)
=> 0 < 3x < π)
Therefore, f3 is strictly decreasing in interval![]() .
.
Now, in interval ![]()
f3'(x)=-3sin3x > 0 as ![]()
Therefore, f3 is strictly increasing in interval![]() .
.
(D) Let f4 = tanx
![]()
In interval![]() ,
,
![]()
Therefore, f4 is strictly increasing in interval ![]() .
.
13