Let I be any interval disjoint from [–1, 1]. Prove that the function f given by 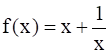 is strictly increasing on 1.
is strictly increasing on 1.
It is given that ![]()
![]()
Now, f’(x) =0
![]()
The points x =1 and x = -1 divide the real line in three disjoint intervals
(-∞,-1),(-1,1) and (1,∞)
Now in interval, (-1,1)
it is clear that -1 < x < 1
⇒ x2 < 1
![]()
![]()
Therefore, f’(x) = 1-![]() < 0 (-1,1) ~ {0}
< 0 (-1,1) ~ {0}
Therefore, f is strictly decreasing on (-1,1) ~ {0}
x < -1 or 1 < x
⇒ x2 > 1
![]()
![]()
Therefore, f’(x) = 1-![]() > 0 (-∞, -1) and (1,∞)
> 0 (-∞, -1) and (1,∞)
Therefore, f is strictly increasing in interval I disjoint from (-1,1)
Hence Proved.
15