Prove that the function f given by f (x) = log sin x is strictly increasing on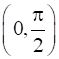 
and strictly decreasing on 
.
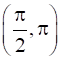It is given that f (x) = log sin x
In interval
, f’(x) = cot x >0
Therefore, f is strictly increasing in
.
In interval
, f’(x) = cot x < 0
Therefore, f is strictly decreasing in
.
17