Find the equation of all lines having slope 2 which are tangents to the curve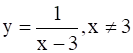

Question

Philoid · Accepted Answer

It is given that equation of the curve y =

Now, slope of the tangent to the given curve at a point (x,y) is:

Now, if the slope of the tangent is 2, then we get,

⇒ 2(x-3)² = -1

⇒ (x-3)² =

This is not possible since the L.H.S. is positive while the R.H.S. is negative.

Therefore, there is no tangent to the given curve having a slope 2.