It is given that ay² = x³

Now, differentiating both sides with respect to x, we get

Then, the slope of the tangent to the given curve at (am², am³) is

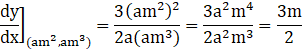
Then, slope of normal at (am², am³)

=

Therefore, equation of the normal at (am², am³) is given by:

y - am³ =

⇒ 3my – 3am⁴ = -2x + 2am²

⇒ 2x + 3my – am²(2 + 3m²) = 0

Therefore, equation of the normal at (am², am³) is 2x + 3my – am²(2 + 3m²) = 0