Using differentials, find the approximate value of each of the following up to 3 places of decimal.

Question

Philoid · Accepted Answer

Consider y =

Let x = 0.008 and Δx = 0.001. Then, we get

Δy = (x+∆x)^1/3 - (x)^1/3

= (0.009)^1/3 - (0.008)^1/3 = (0.009)^1/3 - 0.2

= (0.009)^1/3 = Δy + 0.2

Now, dy is approximately equal to Δy and is given by:

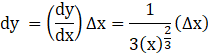
= 0.008

Therefore, the approximate value of is 0.008.