Find the intervals in which the function f given by
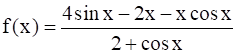
is (i) strictly increasing (ii) strictly decreasing.
(i) It is given that f(x) = ![]()
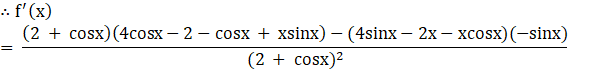
![]()
![]()
![]()
![]()
![]()
![]()
Now, if f’(x) =0
⇒ cos x = 0 or cosx = 4
But, cosx = 4 is not possible
Therefore, cosx =0
⇒ x = ![]()
Now, x =![]() divides (0,2π) into three disjoints intervals
divides (0,2π) into three disjoints intervals
![]()
In the intervals ![]() and
and![]() , f’(x)>0
, f’(x)>0
Therefore, f(x) is increasing for 0< x < ![]() and
and ![]() < x < 2π.
< x < 2π.
In interval![]() , f’(x)<0
, f’(x)<0
Therefore, f(x) is decreasing for ![]() < x <
< x < ![]() .
.
9