Find the maximum area of an isosceles triangle inscribed in the ellipse 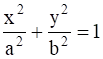 with its vertex at one end of the major axis.
with its vertex at one end of the major axis.
It is given that ellipse ![]()
Let the major axis be along the x – axis.1).
Let ABC be the triangle inscribed in the ellipse where vertex C is at (a,0).
Since, the ellipse is symmetrical w.r.t. x - axis and y - axis, we can assume the coordinates of A to be ( - x1,y1) and the coordinates of B to be ( - x1, - y1).
Now, we have y1 = ± ![]()
Therefore, Coordinates of A ![]() and the coordinates of B
and the coordinates of B![]()
As the point(x1,y1) lies on the ellipse, the area of triangle ABC (A) is given by:
A = ![]()
![]() ……..(1)
……..(1)
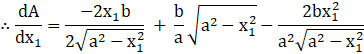
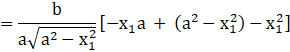
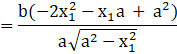
Now, ![]()
![]()
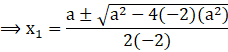
![]()
![]()
![]()
But, x1 cannot be equal to a.
⇒ x1 = ![]()
y1 = ![]()
Now, 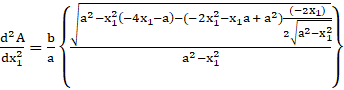
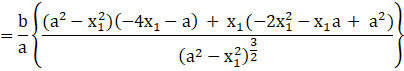
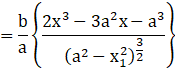
Also, when x1 = ![]() , then,
, then,
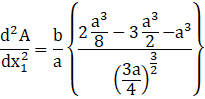
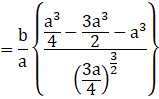
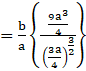 < 0
< 0
Then, the area is the maximum when x1 = ![]() .
.
Therefore, Maximum area of the triangle is given by:
A = ![]()
![]()
![]()
![]()