Let x and y be the length and breadth of the rectangular window.

Radius of the semi - circular opening =

It is given that the perimeter of the window is 10m.

⇒ x + 2y +

Therefore, Area of the window (A) is given by

=

Now, , then

=0

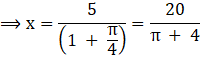
Then, when x = then < 0.

Therefore, by second derivative test, the area is maximum when length

x = m.

Now, y =

Therefore, the required dimensions of the window to admit maximum light is given by length = m and breadth =m.