Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is .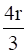

Question

Philoid · Accepted Answer

Let R and h be the radius and the height of the cone respectively.

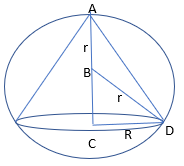
The volume (V) of the cone is given by;

V =

Now, from the right triangle BCD, we get,

BC =

V =

Now, if , then,

Now,

Now, when , it can be shown that < 0.

Therefore, the volume is the maximum when .

When,

Height of the cone = r + .

Therefore, it can be seen that the altitude of the circular cone of maximum volume that can be inscribed in a sphere of radius r is.