Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 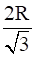. Also find the maximum volume.

Question

Philoid · Accepted Answer

Let r and h be the radius and the height of the cylinder respectively.

Now, h =

The volume (V) of the cylinder is given by:

V = πr²h =2 πr²

Now, if

Now,

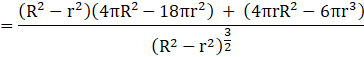
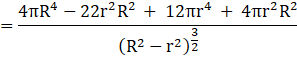
Now, we can see that at, , < 0.

Therefore, the volume is the maximum when.

When , the height of the cylinder is .

Therefore, the volume of the cylinder is the maximum when the height of the cylinder is .

Hence Proved.