It is given that the equation of the curve is 9y² = x³

Differentiating w.r.t. x, we get,

The slope of the normal to the given curve at point (x₁,y₁) is

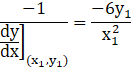
Then, the equation of the normal to the curve at (x₁,y₁)is

⇒ y – y₁ =

⇒

⇒

⇒

⇒

Now, it is given that the normal makes equal intercepts with the axes.

Thus, we get,

⇒

⇒

⇒ …………………….(1)

Since, the point (x₁,y₁)lies on the curve …………(2)

From (1) and (2), we get

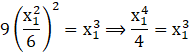
Now putting the value of x₁ in (2), we get

Therefore, the required points are