Evaluate 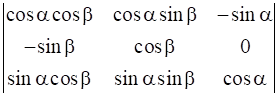
Let Δ = 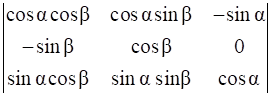
Expanding along C3 we get
Δ = -sinα (-sinβ × sinα sinβ – cosβ × sinα cosβ) – 0 (sinα cosβ × cosα sinβ – cosα cosβ × sinα sinβ) + cosα (cosα cosβ × cosβ – cosα sinβ × (-sinβ))
Δ = -sinα (-sinα sin2β – sinα cos2β) – 0 + cosα (cosα cos2β + cosα sin2β)
Δ = sinα × sinα (sin2β + cos2β) + cosα × cosα (cos2β + sin2β)
[Taking –sinα and cosα common]
Since, sin2β + cos2β = 1
∴ Δ = sin2α + cos2α
Δ = 1 [sin2α + cos2α = 1]
4