If a, b and c are real numbers, and
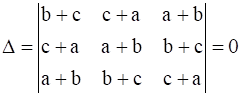
Show that either a + b + c = 0 or a = b = c.
Given, Δ = 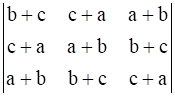
Applying Elementary transformations, we get
R1→ R1 + R2 + R3 we have,
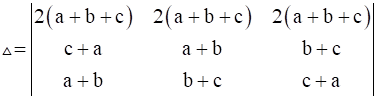
Δ = 2 (a + b + c) 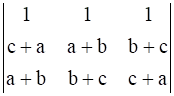
Now applying C2→ C2 – C1 and C3→ C3 – C1
Δ = 2 (a + b + c) 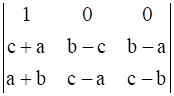
Expanding along R1
Δ = 2 (a + b + c) [1 {(b – c)(c – b) – (b – a)(c – a)} – 0 + 0]
Δ = 2 (a + b + c) [- b2 – c2 + 2bc – bc + ba + ac – a2]
Δ = 2 (a + b + c) [ab + bc + ca – a2 – b2 – c2]
Given that Δ = 0
∴ 2 (a + b + c) [ab + bc + ca – a2 – b2 – c2] = 0
⇒ Either a + b + c = 0, or ab + bc + ca – a2 – b2 – c2 = 0
Now
ab + bc + ca – a2 – b2 – c2 = 0
Multiplying both sides by -2
⇒ - 2ab – 2bc – 2ca + 2a2 + 2b2 + 2c2 = 0
⇒ a2 – 2ab + b2 + b2 – 2bc + c2 + c2 – 2ca + a2 = 0
⇒ (a – b)2 + (b – c)2 + (c – a)2 = 0
Since, (a – b)2, (b – c)2, (c – a)2 are non-negative
∴ (a – b)2 = (b – c)2 = (c – a)2
⇒ (a – b) = (b – c) = (c – a)
⇒ a = b = c
Hence, if ∆ = 0, then either a + b + c = 0 or a = b = c