Let 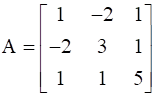 . Verify that
. Verify that
[adj A]-1 = adj (A-1)
A = 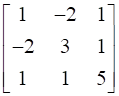
|A| = 1 (3 × 5 – 1 × 1) – (-2) ((-2) × 5 – 1 × 1) + 1 ((-2) × 1 – 3 × 1)
|A| = (15 – 1) + 2 (-10 – 1) + (-2 – 3)
|A| = 14 – 22 – 5 = -13
To find the inverse of a matrix we need to find the Adjoint of that matrix
For finding the adjoint of the matrix we need to find its cofactors
Let Aij denote the cofactors of Matrix A
Minor of an element aij = Mij �
a11 = 1, Minor of element a11 = M11 = 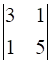 = (3 × 5) – (1 × 1) = 14
= (3 × 5) – (1 × 1) = 14
a12 = -2, Minor of element a12 = M12 = 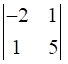 = (-2 × 5) – (1 × 1) = -11
= (-2 × 5) – (1 × 1) = -11
a13 = 1, Minor of element a13 = M13 = 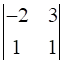 = (-2 × 1) – (3 × 1) = -5
= (-2 × 1) – (3 × 1) = -5
a21 = -2, Minor of element a21 = M21 =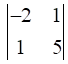 = ((-2) × 5) – (1 × 1) = -11
= ((-2) × 5) – (1 × 1) = -11
a22 = 3, Minor of element a22 = M22 = 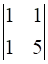 = (1 × 5) – (1 × 1) = 4
= (1 × 5) – (1 × 1) = 4
a23 = 1, Minor of element a23 = M23 = 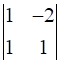 = (1 × 1) – ((-2) × 1) = 3
= (1 × 1) – ((-2) × 1) = 3
a31 = 1, Minor of element a31 = M31 = 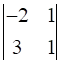 = (-2 × 1) – (3 × 1) = -5
= (-2 × 1) – (3 × 1) = -5
a32 = 1, Minor of element a32 = M32 = 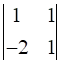 = (1 × 1) – (1 × (-2)) = 3
= (1 × 1) – (1 × (-2)) = 3
a33 = 5, Minor of element a33 = M33 = 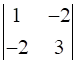 = (1 × 3) – ((-2) × (-2)) = -1
= (1 × 3) – ((-2) × (-2)) = -1
Cofactor of an element aij = Aij
A11 = (-1)1+1× 14 = 1 × 14 = 14
A12 = (-1)1+2× (-11) = (-1) × (-11) = 11
A13 = (-1)1+3× (-5) = 1 × (-5) = -5
A21 = (-1)2+1× (-11) = (-1) × (-11) = 11
A22 = (-1)2+2 × 4 = 1 × 4 = 4
A23 = (-1)2+3 × 3 = (-1) × 3 = -3
A31 = (-1)3+1 × (-5) = 1 × (-5) = -5
A32 = (-1)3+2 × 3 = (-1) × 3 = -3
A33 = (-1)3+3 × (-1) = 1 × (-1) = -1
Adj A = 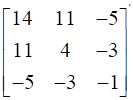 =
= 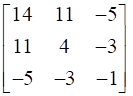
A-1 = (Adj A)/|A|
A-1 = 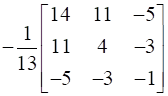 =
= 
(i) |Adj A| = 14(-4 – 9) – 11 (-11 – 15) – 5 (-33 + 20)
= 14 × (-13) – 11 × (-26) – 5 (-13)
= -182 + 286 + 65 = 169
Similarly Finding the Adj (Adj A) as found above
Adj (Adj A) = 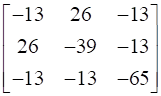
[Adj A]-1 = Adj (Adj A)/|Adj A|
= 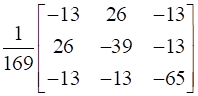
= 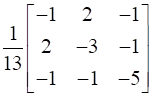
A-1 = 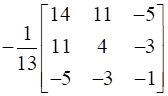 =
= 
Similarly Finding the Adj (A-1) as found above
Adj (A-1) = 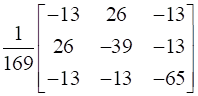 =
= 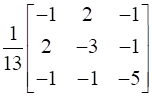
Hence, [Adj A]-1 = Adj (A-1)