Prove that 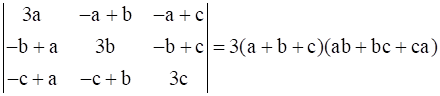
Let Δ = 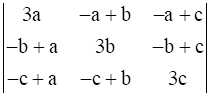
Applying Elementary Transformations
C1→ C1 + C2 + C3, we have
Δ = 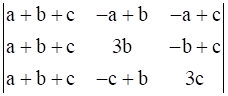
Taking (a + b + c) common from C1, we get
Δ = (a + b + c)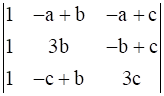
Applying R2→ R2 – R1 and R3→ R3 – R1
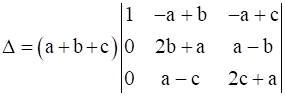
Expanding along C1
Δ = (a + b + c) [1 × {(2b + a) (2c + a) – (a – b) (a – c)} – 0 + 0]
Δ = (a + b + c) [4bc + 2ab + 2ac + a2 – a2 + ac + ba – bc]
Δ = (a + b + c) (3ab + 3bc + 3ac)
Δ = 3 (a + b + c) (ab + bc + ca)
Hence, the given result proved.
13