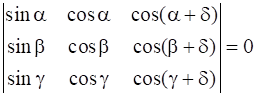
Let Δ =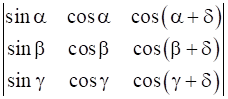

Δ =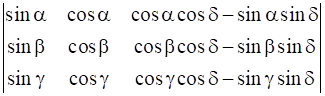

Δ =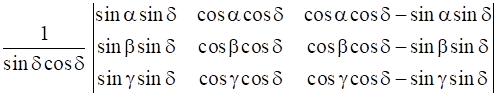

Applying Elementary Column Transformations

C₁→ C₁ + C₃

Δ =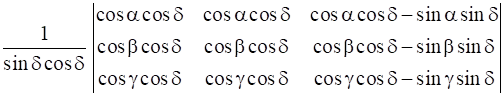

Since, the two columns are identical

[In a determinant if two columns are identical the the value of determinant is 0]

So, the value of given determinant is 0

∴ Δ = 0

Hence, the given result is proved.