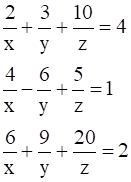
Given System of equations are

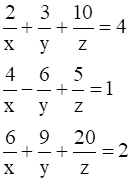
Let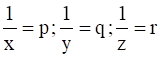

∴ Given system of equation becomes

2p + 3q + 10r = 4

4p – 6q + 5r = 1

6p + 9q – 20r = 2

The given System of Equations can be written in the form of AX = B

Here A = 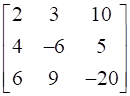and B = 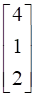, X =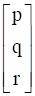

Now we need to find |A|

∴ |A| = 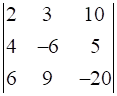= 2 × (120 – 45) – 3 × (- 80 – 30) + 10 × (36 + 36)

= 150 + 330 + 720

= 1200

Since, |A| ≠ 0

∴ A is non-singular. So, it’s inverse exists

Cofactor of an element a_ij = A_ij

A₁₁ = (-1)¹⁺¹× 75 = 1 × 75 = 75

A₁₂ = (-1)¹⁺²× (-110) = (-1) × (-110) = 110

A₁₃ = (-1)¹⁺³× 72 = 1 × (72) = 72

A₂₁ = (-1)²⁺¹× (-150) = (-1) × (-150) = 150

A₂₂ = (-1)²⁺² × (-100) = 1 × (-100) = -100

A₂₃ = (-1)²⁺³ × 0 = (-1) × 0 = 0

A₃₁ = (-1)³⁺¹ × 75 = 1 × 75 = 75

A₃₂ = (-1)³⁺² × (-30) = (-1) × (-30) = 30

A₃₃ = (-1)³⁺³ × (-24) = 1 × (-24) = -24

Adj A = =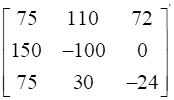

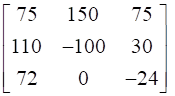
A^-1 = (Adj A)/|A|

A^-1 =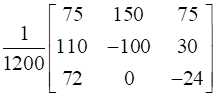

Now,

Since, AX = B

∴ X = A^-1B

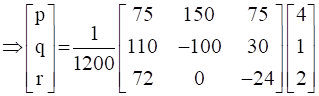
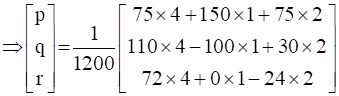
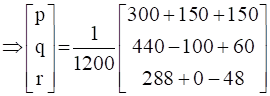
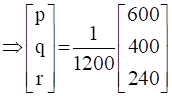
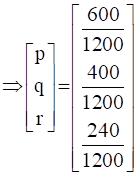
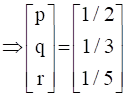
∴ p = �, q = 1/3, r = 1/5

∴ x = 1/p = 2; y = 1/q = 3; z = 1/r = 5

So, x = 2; y = 3; z = 5