If a, b, c, are in A.P, then the determinant 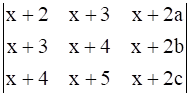is

Question

Philoid · Accepted Answer

Let Δ =

Since, a, b, c are in A.P.

∴ 2b = a + c

Δ =

Applying Elementary Row Transformations

R₁→ R₁ – R₂ and R₃→ R₃ – R₂

Δ =

R₁→ R₁ + R₃, we have

Δ =

[In a determinant if all elements of a row is 0 then the value of determinant is 0.]

So, here all the elements of first row (R₁) are zero.

∴ Δ = 0