If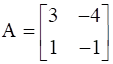 
then prove that 
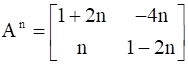where n is any positive integer.
We will be proving the above equation by putting different values of n. Because n is a positive integer so it will take values which are greater than 0 i.e. n = 1, 2, 3 …n
For n=1,
L.H.S = An = A1 = A =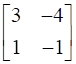 
R.H.S =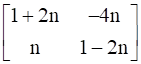 
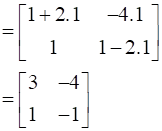
∴ L.H.S = R.H.S
For n=2,
L.H.S = A2
= A.A
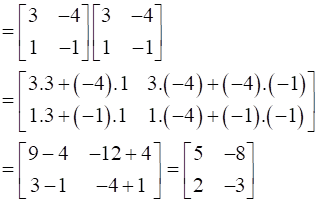
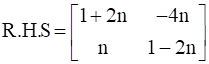
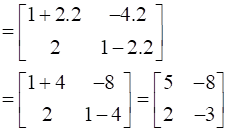
∴ L.H.S = R.H.S
For n = 3,
L.H.S = A3
= A2.A
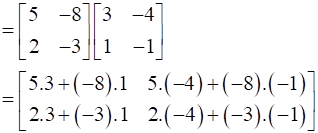
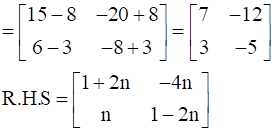
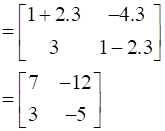
∴ L.H.S = R.H.S
For n = 4,
L.H.S = A4
= A3.A
=
=
=
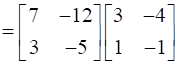
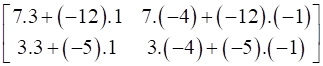
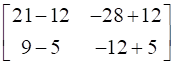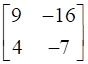
R.H.S =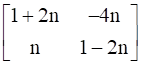 
=
=
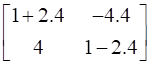
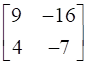
∴ L.H.S = R.H.S
And so on for other values of n.
If we notice each result then we will see that it is of same type that we are trying to prove.
So we can generalise the above results for all positive integer values of n.
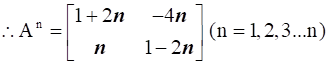
Hence Proved
3