A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below:

(a) If unit sale prices of x, y and z are Rs. 2.50, Rs. 1.50 and Rs. 1.00, respectively, find the total revenue in each market with the help of matrix algebra.
(b) If the unit costs of the above three commodities are Rs. 2.00, Rs. 1.00 and 50 paise respectively. Find the gross profit.
(a) Given the unit sale prices of x, y and z as Rs. 2.50, Rs. 1.50 and Rs. 1.00 respectively.
Unit sale prices can be represented in form of matrix as: 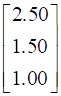
Calculating total revenue in market I:
Number of products in the form of matrix:![]()
So the total revenue is given by:
=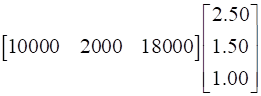
=![]()
=![]()
=![]()
∴ Total revenue in market is Rs 46000.
Calculating total revenue in market II:
Number of products in the form of matrix: ![]()
So the total revenue is given by:
=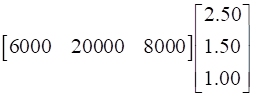
=![]()
=![]()
=![]() .
.
∴ Total revenue in market is Rs. 53000.
(b) Given the unit cost prices of x, y and z as Rs. 2.00, Rs. 1.00 and 50 paisa respectively.
Calculating gross profit in market I:
Unit cost prices can be represented in form of matrix as: 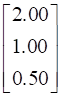
So the total cost of products in market I is given by:
=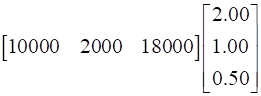
=![]()
=![]()
Since the total revenue in market I is Rs. 46000, the gross profit in this market is given by:
(Rs. 46000 – Rs. 31000)
= Rs. 15000.
Calculating gross profit in market II:
The total cost of products in market II is given by:
=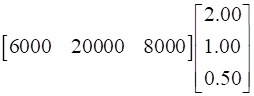
=![]()
=![]()
=![]()
Since the total revenue in market II is Rs. 53000, the gross profit in this market is given by:
(Rs. 53000 – Rs. 36000)
= Rs. 17000.