Find the matrix X so that 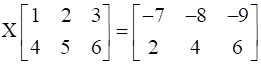
Given X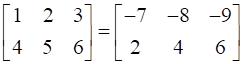
From above equation it can be observed that matrix on R.H.S is a 2×3 matrix and that on the L.H.S is also a 2×3 matrix. Therefore, X must be a 2×2 matrix.
Let X 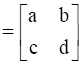
So the equation is given by:
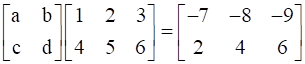
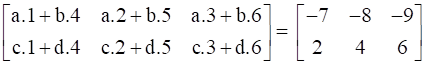
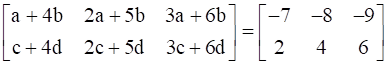
Now equating the corresponding elements of both the matrices we get,
a + 4b = -7, 2a + 5b = -8, 3a + 6b = -9
c + 4d = 2, 2c + 5d = 4, 3c + 6d = 6
Now, a + 4b = -7 ![]() ⇒ a = -4b -7
⇒ a = -4b -7
∴ 2a + 5b = -8 ⇒ 2.(-4b -7) + 5b = -8
⇒ -8b -14 + 5b = -8
⇒ -3b = 6
⇒ b = -2
∴ a = -4b -7 ⇒ a = -4.(-2) -7
⇒ a = 1
Now, c + 4d = 2 ⇒ c = -4d + 2
∴ 2c + 5d = 4 ⇒ 2.(-4d + 2) + 5d = 4
⇒ -8d + 4 + 5d = 4
⇒ -3d = 0
⇒ d = 0
∴ c = -4d + 2 ⇒ c = -4.0 + 2
⇒ c = 2
Thus, a = 1, b = -2, c = 2, d = 0.
Hence X becomes 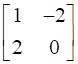
12