The experiemental data for decomposition of N2O5
[2N2O5→ 4NO2 + O2]
in gas phase at 318 k are given below:
t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
102 × [N2O5]/mol L-1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
(i) plot N2O5 against t
(ii) Find the half-life period for the Reaction.
(iii) Draw a graph between log[N2O5]and t.
(iv) what is the rate law?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii)
(i) 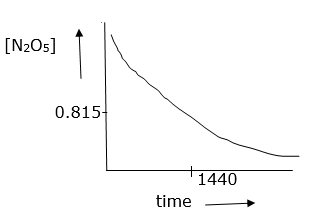
(ii) initial conc.is 1.63 × 10-2 so half conc. is 0.815 × 10-2M From given information and graph t1/2 is 1440 sec.
(iii) 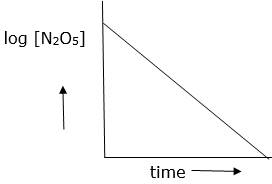
(iv) As log [N2O5] vs time is straight line given reaction is first order. Hence its rate law will be, Rate = k[N2O5]
(v) The slope of above graph is slope = 0.000209
K = 2.303 × slope
⇒ 4.82 × 10-4sec-1
Now, t1/2 = 0.693/K.
⇒ 0.693/4.82 × 10-4
⇒ t1/2 = 1438 sec. which is almost equal to (ii)