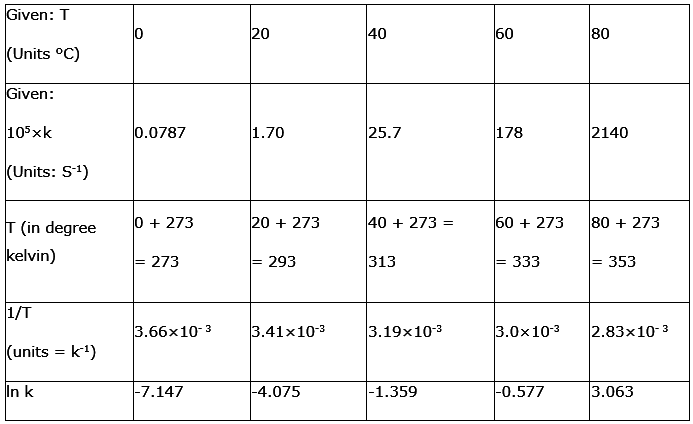
The rate constant for the decomposition of N2O5 at various temperatures is given below:
T/°C | 0 | 20 | 40 | 60 | 80 |
105 × k/s-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and 1/T and calculate the values of A and Ea. Predict the rate constant at 30° and 50°C.
To convert the temperature in °C to °K we add 273 K.

The graph is given as:
The Arrhenius equation is given by k = Ae-Ea/RT
Where, k- Rate constant
A- Constant
Ea-Activation Energy
R- Gas constant
T-Temperature
Taking natural log on both sides,
ln k = ln A-(Ea/RT)
→ equation 1
By plotting a graph, ln K Vs 1/T, we get y-intercept as ln A and Slope is –Ea/R.
Slope = (y2-y1)/(x2-x1)
By substituting the values, slope = -12.301
⇒ –Ea/R = -12.301
But, R = 8.314 JK-1mol-1
⇒ Ea = 8.314 JK-1mol-1 × 12.301 K
⇒ Ea = 102.27 kJ mol-1
Substituting the values in equation 1 for data at T = 273K
⇒ ![]()
⇒ ![]()
(∵ At T = 273K, ln k = -7.147)
On solving, we get ln A = 37.911
∴ A = 2.91×106
When T = 300C, hence T = 30 + 273 = 303K
⇒ ![]()
⇒ ![]()
⇒ ln k = -2.8
⇒ k = 6.08x10-2s-1.
When T = 500C, hence T = 50 + 273 = 323K
Substituting in equation 1,
A = 2.91 × 106, Ea = 102.27 kJ mol-1
Ln K = ln(2.91 × 106)- 102.27/(8.314 × 323)
Thus, ln k = -0.5 and k = 0.607s-1.