Prove that the following functions do not have maxima or minima:

Question

Prove that the following functions do not have maxima or minima: h(x) = x 3 + x 2 + x +1

Philoid · Accepted Answer

h(x) = x³ + x² + x +1

⇒ h’(x) = 3x² + 2x +1

h(x) = 0

⇒ 3x² + 2x +1 = 0

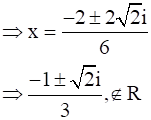
Therefore, there does not exist c ϵ R such that h’(c) = 0

Hence, function h does not have maxima or minima.