Find the maximum profit that a company can make, if the profit function is given by

Question

Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 72x – 18x 2

Philoid · Accepted Answer

It is given that the profit function p(x) = 41 – 72x – 18x²

⇒ p’(x) = -24 – 36x

and p’’(x) = -36

Now, g’(x) = 0

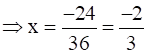
and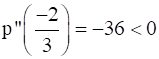

Then, by second derivative test,

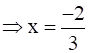is point of local maxima of p.

Therefore, Maximum Profit =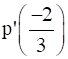

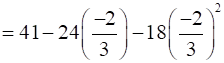
= 41 + 16 – 8

= 49

Therefore, the maximum profit that the company can make is 49 units.