At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
It is given that f (x) = sin2x, x ∈ [0, 2π]
f’(x) = 2cos2x
Now, f’(x) = 0
⇒ cos2x = 0
⇒ 2x = 0
⇒ x = 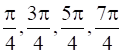
Now, we evaluate the value of f at critical point x = 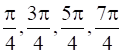 and at end points of the interval [0, 2π]
and at end points of the interval [0, 2π]
f’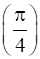 =
= 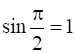
f’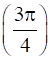 =
= 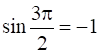
f’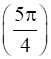 =
= 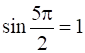
f’ =
= 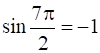
f(0) = sin0, f(2π) = sin2π = 0
Therefore, we have the absolute maximum value of f on [0, 2π] is 1 occurring at
x =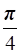 and x =
and x =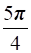 .
.
10