Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
Let r be the radius and h be the height of the cylinder.
Then, the surface area (S) of the cylinder is given by:
S = 2πr2 + 2πrh
⇒ h 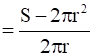
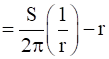
Let V be the volume of the cylinder. Then
V = πr2h
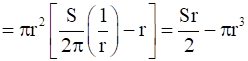
Now, 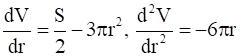
If 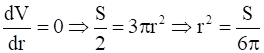
So, when 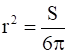 then
then 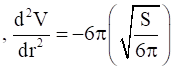 <0
<0
Then, by second derivative test, the volume is the maximum when 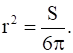
Now, when 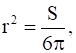 . then h =
. then h = 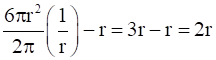
Therefore, the volume is the maximum when the height is the twice the radius or height is equal to diameter.
25