Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Let r be the radius and h be the height of the cylinder.
Let V be the volume of the cylinder. Then
V = πr2h = 100(given)
⇒ h = 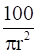
hen, the surface area (S) of the cylinder is given by:
S = 2πr2 + 2πrh
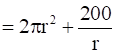
Now, 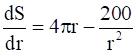 ,
, 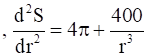 <0
<0
If 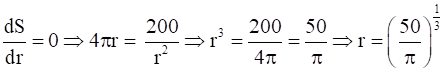
So, when 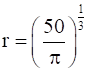 then
then 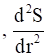 > 0
> 0
Then, by second derivative test, the surface area is the minimum when 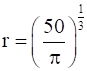
Now, when 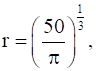 then h =
then h = 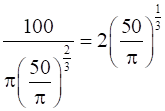 cm.
cm.
Therefore, the dimensions of the can which has the minimum surface area are 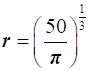 and h
and h 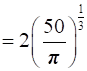 cm.
cm.
22