Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 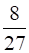 of the volume of the sphere.
of the volume of the sphere.
Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.
Let V be the volume of cone.
Then, V= 
And height of cone h = R + ![]()

Now, 





Now, if, 
After solving this we get, 
So, when,  , then
, then  < 0
< 0
Then, by second derivative test, the volume of the cone is the maximum when 
So, when,  , h = R +
, h = R +
Therefore, V = 

Therefore, the volume of the largest cone that can be inscribed in the sphere is  the volume of the sphere.
the volume of the sphere.
24