Let Ɵ be the semi- vertical angle of the cone.

Let r, h and l be the radius, height and the slant height of the cone respectively.

It is given that slant height is constant.

Now, r = lsinƟ and h = lcosƟ

Then, the volume of the cone (V)

V =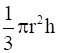

.

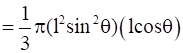
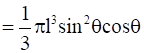
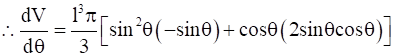
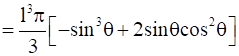
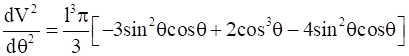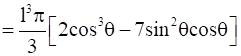
Now, if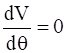

sin³Ɵ = 2sinƟcos²Ɵ

⇒ tan²Ɵ = 2

⇒ tanƟ = √2

⇒

Now, when, then tan²Ɵ = 2 or sin²Ɵ = 2cos²Ɵ.

Then, we get

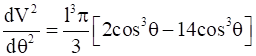
= -4πl³cos³Ɵ < 0 for Ɵ ϵ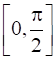

Then, by second derivative test, the volume (V) is the maximum when

Therefore, the semi-vertical angle of the cone of the maximum volume and of given slant height is .

Hence Proved.