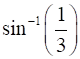We know that total surface area of the cone = S = πr(l + r) …(1)

and Volume of the cone(V) =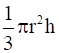

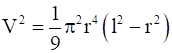
Then by (1), we get,

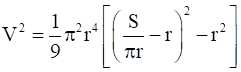
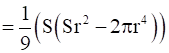
P = V²

Now, differentiating P with respect to r, we get,

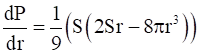
Now, if, 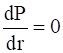, then

S = 4πr²

Now again differentiating with respect to r, we get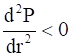

Therefore, P is maximum when S = 4πr²

And V is maximum when S = 4πr²

⇒ πr(l + r) = 4πr²

⇒ l = 3r

SinƟ =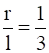

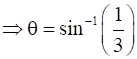
Therefore, semi-vertical angle of right circular cone of given surface area and maximum volume is .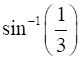

Hence Proved.