It is given that x² = 2y

For each value of x, the position of the point will be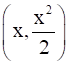

The distance d(x) between the points and (0,5) is given by:

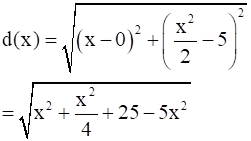
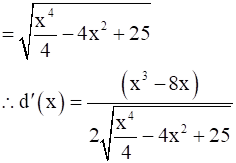
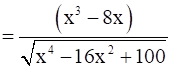
d’(x) = 0

⇒ x³ – 8x = 0

⇒ x(x²-8) =0

⇒ x = 0,

And, .

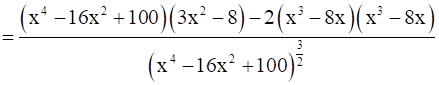
So, now when x = 0, then d’’(x) = < 0

And when, x = , d’’(x) >0

Then, by second derivative test, d(x) is minimum at

So, when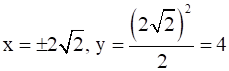

Therefore, the point on the curve x2 = 2y which is nearest to the point (0,5) is .