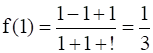For all real values of x, the minimum value of 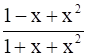 is
is
Let 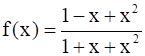
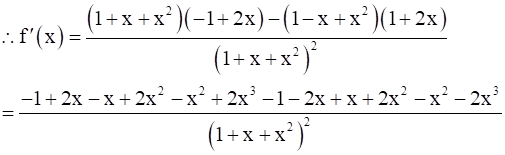
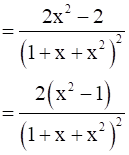
Then, f’(x) = 0
⇒ x2 = 1
⇒ x = �1
Now, 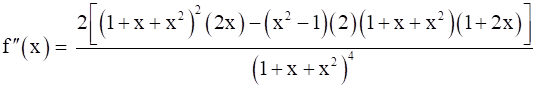
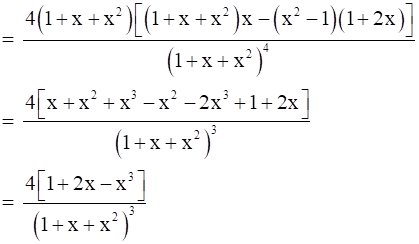
And, 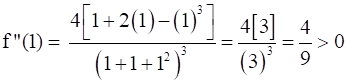
Also, f’’(-1) = -4 < 0
Then, by second derivative test, f is minimum at x = 1 and the minimum value is given by
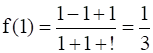
29
For all real values of x, the minimum value of 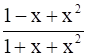 is
is
Let 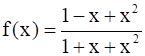
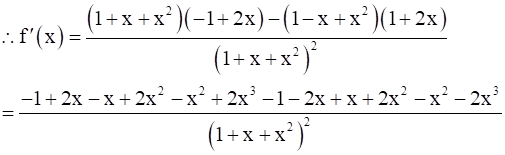
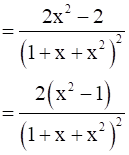
Then, f’(x) = 0
⇒ x2 = 1
⇒ x = �1
Now, 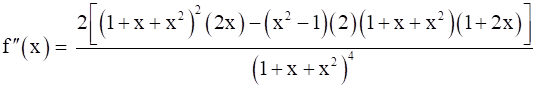
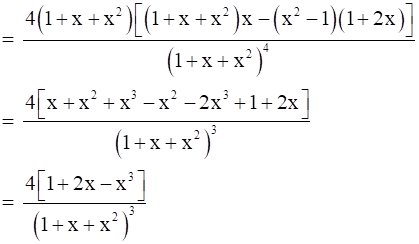
And, 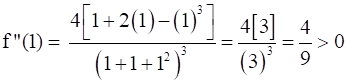
Also, f’’(-1) = -4 < 0
Then, by second derivative test, f is minimum at x = 1 and the minimum value is given by