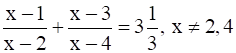
Given:

taking LCM

cross multiplying

3x² - 15x + 15 = 5x² - 30x + 40

2x² - 15x + 25 = 0

Using the splitting middle term - the middle term of the general equation is divided in two such values that:

Product = a.c

For the given equation a = 2 b = - 15 c = 25

= 2.25 = 50

And either of their sum or difference = b

= - 15

Thus the two terms are - 10 and - 5

Sum = - 10 - 5 = - 15

Product = - 10. - 5 = 50

2x² - 15x + 25 = 0

2x² - 10x - 5x + 25 = 0

2x(x - 5) - 5(x - 5) = 0

(x - 5)(2x - 5) = 0

(x - 5) = 0 or (2x - 5) = 0

Hence the roots of equation are