RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 10. Quadratic Equations

Subject: Maths - Class 10th

Q. No. 21 of Exercise 10D

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

21

If the roots of the equation (a2 + b2)x2 – 2 (ac + bd)x + (c2 + d2) = 0 are a c equal, prove that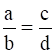

Given the roots of the equation are equation (a2 + b2)x2 – 2 (ac + bd)x + (c2 + d2) = 0 are equal.

Comparing with standard quadratic equation ax2 + bx + c = 0


a = (a2 + b2) b = – 2(ac + bd) c = (c2 + d2)


For real and distinct roots: D = 0


Discriminant D = b2 – 4ac = 0


[ – 2(ac + bd)]2 – 4(a2 + b2)(c2 + d2) = 0


4(a2c2 + b2d2 + 2abcd) – 4(a2c2 + a2d2 + b2c2 + b2d2) = 0


using (a + b)2 = a2 + 2ab + b2


4(a2c2 + b2d2 + 2abcd – a2c2 – a2d2 – b2c2 – b2d2) = 0


2abcd – a2d2 – b2c2 = 0


– (2abcd + a2d2 + b2c2) = 0


(ad – bc)2 = 0


ad = bc



Hence proved.


Chapter Exercises

Exercise 10A
Exercise 10B
Exercise 10C
Exercise 10D
Exercise 10E
Exercise 10F

More Exercise Questions

1

Find the nature of the roots of the following quadratic equations:

2x2 – 8x + 5 = 0
1

Find the nature of the roots of the following quadratic equations:

3x2 –2√6x + 2 = 0
1

Find the nature of the roots of the following quadratic equations:

5x2 – 4x + 1 = 0
1

Find the nature of the roots of the following quadratic equations:

5x (x – 2) + 6 = 0
1

Find the nature of the roots of the following quadratic equations:

12x2 – 4√15x + 5 = 0
1

Find the nature of the roots of the following quadratic equations:

x2 – x + 2 = 0
2

If a and b are distinct real numbers, show that the quadratic equation 2 (a2 + b2)x2 + 2(a + b)x + 1 = 0 has no real roots.
3

Show that the roots of the equation x2 + px – q2 = 0 are real for all real values of p and q.
4

For what values of k are the roots of the quadratic equation 3x2 + 2kx + 27 = 0 real and equal?
5

For what value of k are the roots of the quadratic equation kx(x –2√5) + 10 = 0 real and equal?
6

For what values of p are the roots of the equation 4 x2 + px + 3 = 0 real and equal?
7

Find the nonzero value of k for which the roots of the quadratic equation 9x2 – 3kx + k = 0 are real and equal.
8

Find the values of k for which the quadratic equation (3k + 1) x2 + 2(k + 1)x + 1 = 0 has real and equal roots.
9

Find the values of p for which the quadratic equation (2p + 1)x2 – (7p + 2)x + (7p – 3) = 0 has real and equal roots.
10

Find the values of p for which the quadratic equation (p + 1)x2 – 6 (p + 1) x + 3 (p + 9) = 0, p 1 has equal roots. Hence, find the roots of the equation.
11

If – 5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p (x2 + x) + k = 0 has equal roots, find the value of k.
12

If 3 is a root of the quadratic equation x2 – x + k = 0, find the value of p so that the roots of the equation x2 + k (2x + k + 2) + p = 0 are equal.
13

If – 4 is a root of the equation x2 + 2x + 4p = 0, find the value of k for which the quadratic equation x2 + px (1 + 3k) + 7(3 + 2k) = 0 has equal roots.
14

If the quadratic equation (1 + m2)x2 + 2mcx + c2 – a2 = 0 has equal roots, prove that c2 = a2(1 + m2) .
15

If the roots of the equation (c2 – ab)x2 – 2(a2 – bc)x + (b2 – ac) = 0 are real and equal, show that either a = 0 or (a3 + b3 + c3) = 3abc.
16

Find the values of p for which the quadratic equation 2x2 + px + 8 = 0 has real roots.
17

Find the value of a for which the equation (a – 12)x2 + 2(a – 12)x + 2 = 0 has equal roots.
18

Find the value of k for which the roots of 9x2 + 8kx + 16 = 0 are real and equal.
19

Find the values of k for which the given quadratic equation has real and distinct roots:
20

If a and b are real and ab then show that the roots of the equation (a – b)x2 + 5(a + b)x – 2(a – b) = 0 are real and unequal.
21

If the roots of the equation (a2 + b2)x2 – 2 (ac + bd)x + (c2 + d2) = 0 are a c equal, prove that

22

If the roots of the equations ax2 + 2bx + c = 0 and are simultaneously real then prove that b2 = ac.

Students Store