Two pipes running together can fill a tank in 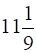minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.

Let the time taken by one pipe to fill the tank be x minutes

The time taken by other pipe to fill the tank = x + 5 minutes


Volume of tank be V


Volume of tank filled by one pipe in x minutes = V


Volume of tank filled by one pipe in 1 minutes = V/x


Volume of tank filled by one pipe in minutes =


Volume of tank filled by other pipe in minutes =


Volume of tank filled by one pipe in minutes + Volume of tank filled by other pipe in minutes = V






200x + 500 = 9x2 + 45x


9x2 – 155x – 500 = 0


Using the splitting middle term – the middle term of the general equation is divided in two such values that:


Product = a.c


For the given equation a = 9 b = – 155 c = – 500


= 9. – 500 = – 4500


And either of their sum or difference = b


= – 155


Thus the two terms are – 180 and 25


Difference = – 180 + 25 = – 155


Product = – 180.25 = – 4500


9x2 – 180x + 25x – 500 = 0


9x(x – 20) + 25(x – 20) = 0


(x – 20) (9x + 25) = 0


(x – 20) = 0 (9x + 25) = 0


x = 20 or x = – 25/9


x = 20 (time cannot be negative fraction)


Hence one pipe fills the tank in 20 mins. and other pipe fills the cistern in (20 + 5) = 25 mins


56